| |
| |
Welcome to the homepage of Prof. Kan-Hao Xue!
We are a research group under the ISMD Lab (Institute of Information Storage Materials and Devices).
Our main reseach goal is to use theoretical approaches for better understanding of the electronic device behaviors, for designing new functional materials, and for multiscale simulation of electrochemical and electronic devices.
Online LDA(GGA)-1/2 and shLDA(shGGA)-1/2 calculations available!
|
|
 |
|
|
|
|
|
Updates:
Aug 28 2023: shell DFT-1/2 for OpenMX: DFT-1/2 and shell DFT-1/2 functionalities for the OpenMX package has been put online.
Aug 28 2023: DFT-1/2 and shell DFT-1/2 services for ABINIT are temporarily stopped.
Apr 11 2021: shell DFT-1/2 for ABINIT: a beta version of the DFT-1/2 and shell DFT-1/2 functionalities for the ABINIT package has been put online. Right now only the ONCVPSP-PBE norm-conserving pseudopotentials are supported.
Aug 26 2020: Fixed the file compression problem in shell DFT-1/2 module: the zip file does not contain unnecessary file paths any more.
Aug 12 2020: Server transferred successfully.
|
|
| |
| |
Highlight:
Do you need a fast yet accurate band gap rectification method for density functional theory (DFT)? A comprehensive review (38 pages) on the DFT-1/2 and shell DFT-1/2 methods has recently been published as an invited contribution on Journal of Physics: Condensed Matter.
(2022j) Ge-Qi Mao, Zhao-Yi Yan, Kan-Hao Xue*, Zhengwei Ai, Shengxin Yang, Hanli Cui, Jun-Hui Yuan, Tian-Ling Ren, and Xiangshui Miao,
DFT-1/2 and shell DFT-1/2 methods: electronic structure calculation for semiconductors at LDA complexity,
Journal of Physics: Condensed Matter
34, 403001 (2022).
|
|
 |
|
| |
For the celebrated DFT-1/2 method [L. G. Ferreira, M. Marques, and L. K. Teles, Physical Review B 78, 125116 (2008)], we start from scratch, the fundamental Hamiltonian in a solid. Then, step-by-step, we show how the procedure of proving the Janak theorem further yields the mathematical formulation of DFT-1/2, as well as the self-energy potential form. The derivation is in great details and is fully consistent with the book
Electronic Structure by Richard Martin. We also review the further developments based on the original DFT-1/2 work of Ferreira, Marques and Teles in 2008. The basic idea of shell DFT-1/2 is clarified. Moreover, we also review the history of electronic band structure calculations, and emphasize the origin of band gap underestimation in the LDA and GGA forms of DFT. The relation of DFT-1/2 with other gap rectification methods, such as hybrid functional, sX-LDA, GW, SIC, Koopmans-compliant functional, scissor's operator, DFT+U, Delta-sol, etc., is presented.
|
Highly recommended for reading!
密度泛函理论虽然已经成为第一原理计算事实上的标准,但其在常见的局域密度近似(LDA)以及广义梯度近似(GGA)下,仍然存在系统性低估半导体带隙的问题。在最近发表的综述论文中,我们回顾了固体能带计算的历史,分析了密度泛函理论带隙问题的根源,建立各种解释之间的联系。特别是,针对巴西圣保罗大学费雷拉教授等人于 2008 年提出的 DFT-1/2 能带计算方法,我们从固体的基本哈密顿量出发进行了详细的数学推导,特别是强调了其自能势形式的物理来源,推导过程的变量标记与 Richard Martin 的 Electronic Structure 经典论著严格保持一致。文章阐明了我们于 2018 年提出的 shell DFT-1/2 改进方法的基本思路与其应用效果,并介绍了 DFT-1/2 的其他重要发展。在带隙修正的层面上,我们还比较了 DFT-1/2 与杂化泛函、sX-LDA、GW、电子自相互作用修正(SIC)、Koopmans-compliant 泛函、剪刀算符、DFT+U、Delta-sol 等其他方法之间的联系与区别。
|
|
| |
| |
| |
Selected Researches
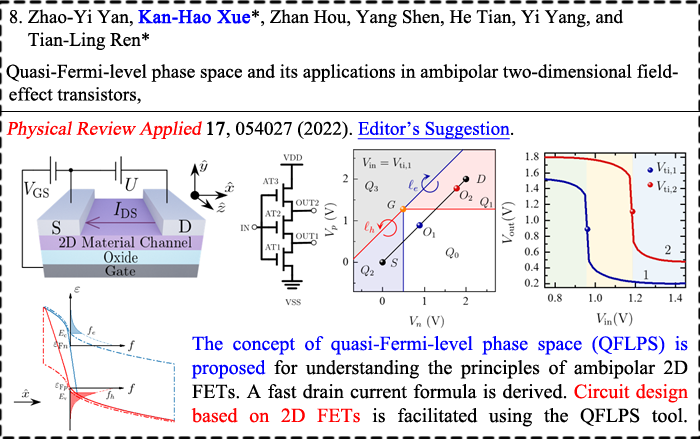
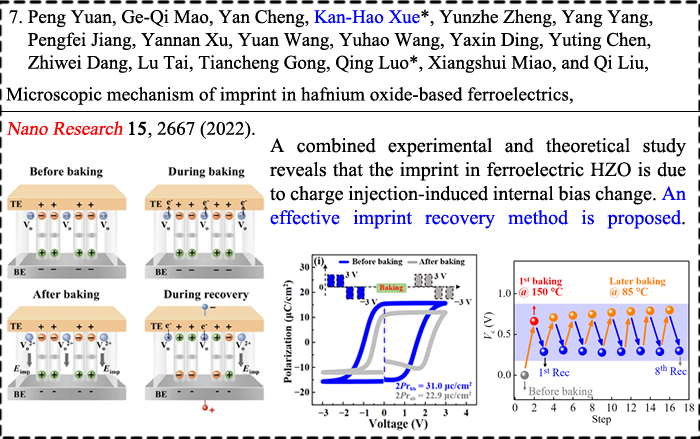
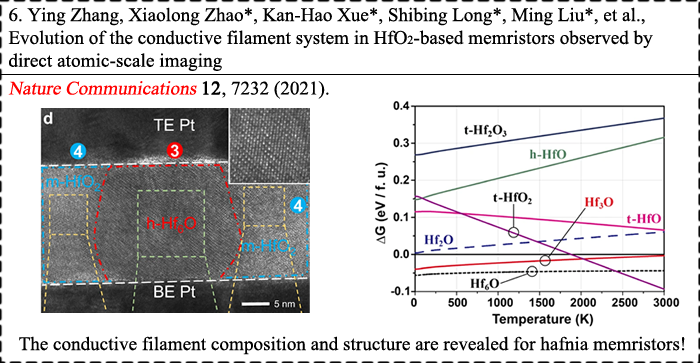
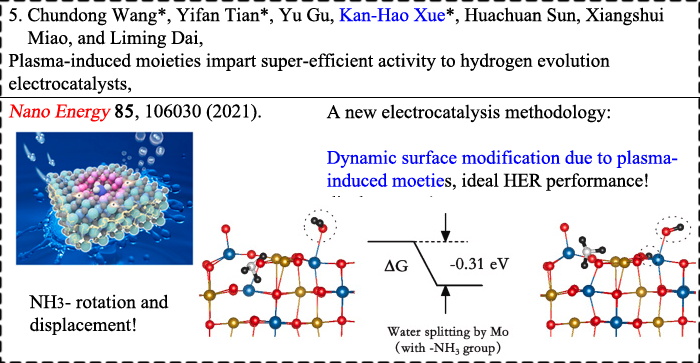
|
|
|
|
| |
| |
Education Background
| Ph. D. |
Electrical Engineering, University of Colorado, Colorado Springs (USA) |
2010 |
| |
科罗拉多大学珂泉分校
Outstanding Graduate Student (1 per Department) |
|
|
| M.S.E.E. |
Microelectronics, Tsinghua University (Beijing, China) 清华大学 |
2007 |
| |
Outstanding Master Graduate of Tsinghua University in 2007 (53 out of 3,768) |
|
|
| B.S.E.E. |
Electronics Engineering, Tsinghua University (Beijing, China) 清华大学 |
2004 |
|
Contact Information
| Kan-Hao Xue (薛堪豪) |
| Email: xkh at hust.edu.cn |
|
|
| |
| |
| |
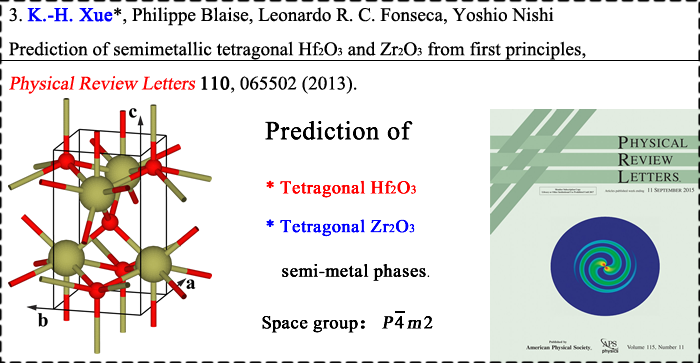
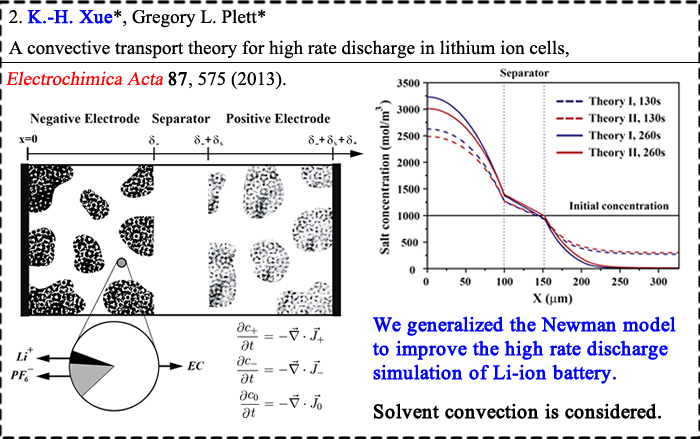
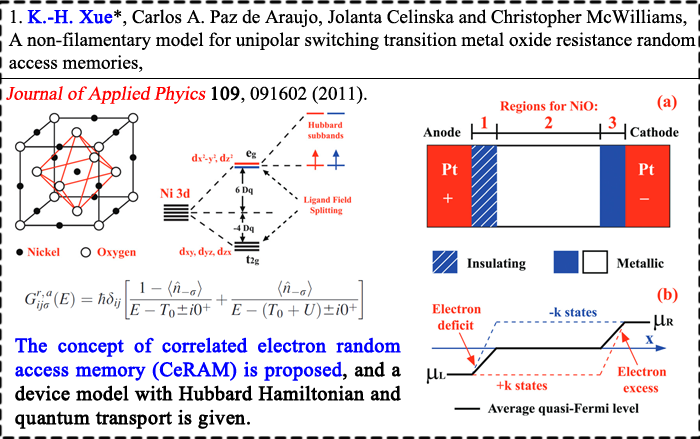
We have applied the density functional theory a lot in our calculations. However, it is well-known that for insulators the band gaps tend to be greatly underestimated by LDA/GGA approximations. For device-level simulation, it is also necessary to establish supercells with more than 500 atoms. Thanks to Prof. L. G. Ferreira and coworkers, the LDA-1/2 (or GGA-1/2) self-energy correction method is extremely powerful in calculating the electronic structures of normal semiconductors (without strong electron correlation effect).
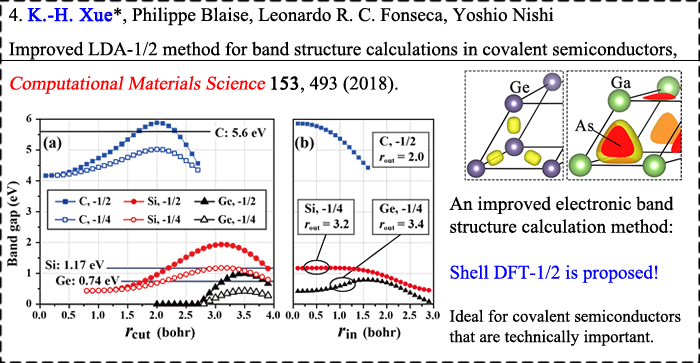
An improved version of LDA-1/2 has been developed for covalent semiconductors, named shell LDA-1/2, or shLDA-1/2 for short.
Our website affords online shLDA-1/2 self-energy correction service.
|
|
 |
|
| |
|



